


Galileu Galilei nasceu no mesmo ano que Shakespeare.
Seu pai inscreveu-o na Universidade de Pisa para estudar medicina, mas Galileu desistiu dois anos depois e decidiu estudar matemática com Otílio Ricci, discípulo do famoso Niccolò Tartaglia. Seu pai tampouco desejava que o filho estudasse matemática clássica e assim Galileu abandonou a universidade em 1585, sem obter o título e foi para Florença, onde deu aulas particulares para sobreviver e continuou os seus estudos de matemática, mecânica e hidrostática.
Em 1588, com o apoio de Guidobaldo del Monte, matemático e admirador da sua obra, Galileu foi nomeado para a cátedra de matemática na Universidade de Pisa.
Em 1592, ainda devido à influência de Guidobaldo del Monte, conseguiu a cátedra de matemática na Universidade de Pádua, onde passou os 18 anos seguintes, ensinando geometria, mecânica e astronomia.
Em Pádua, estudou o movimento realizado por um projétil. O movimento realizado por um projétil, seja uma pedra ou uma bala de canhão, parecia muito complicado na Idade Média. No Renascimento, com o aumento da utilização de canhões de longo alcance, descobriu-se que as concepções aristotélicas não correspondiam ao movimento real da bala.
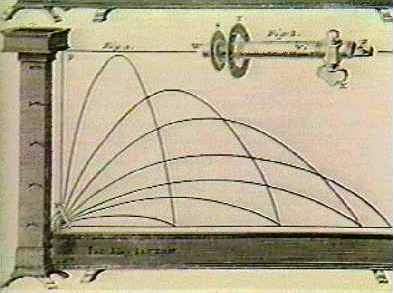
Variando a velocidade horizontal do projétil e a altura de queda, Galileu conseguiu demonstrar que a trajetória desse movimento seguia uma parábola. Formulou as leis do movimento parabólico, e, com isso, conquistou reputação internacional.

Foi Galileu quem teve a brilhante compreensão de que esse movimento podia ser decomposto em dois movimentos independentes, um ao longo do eixo e outro ao longo do eixo. Na figura abaixo, o skatista realiza um movimento de queda livre durante seu salto para cima, mas a componente horizontal da velocidade do skatista é constante, a mesma que o skate, e é por isso que, após o salto, ele cai exatamente sobre o skate.

Em 1609, Galileu, tendo ouvido falar da 'trompa holandesa', um 'instrumento para olhar coisas a distância', constituído por um tubo com uma lente em cada extremidade, construído pelo fabricante de óculos holandes Hans Lippershey, constrói seu primeiro telescópio.

Com ele, começa a fazer observações astronômicas, descobrindo
Em 1910, publicou estas descobertas no livro Sidereus Nuncius ("O Mensageiro das Estrelas"), estrategicamente dedicado a Cosimo II de Medici, à época Grão-Duque da Toscânia. Pelo mesmo motivo, denominou os satélites de Júpiter como Medicea Sidera (estrelas Mediceanas).
Essa homenagem rendeu-lhe a confortável posição de Matemático e Filósofo-chefe do Grão-Duque em Florença, capital do Grão-Ducado, o que lhe garantia a proteção da poderosa família Medici e tempo livre, sem obrigação de dar aulas, para dedicar-se a suas pesquisa.

Essa publicação lhe trouxe fama e o ingresso na prestigiada Accademia dei Lincei. Foi convocado a Roma para apresentar as suas descobertas ao Colégio Romano dos jesuítas, cujos matemáticos eram considerados as maiores autoridades daquele tempo. Lá conheceu o futuro Papa Urbano VIII, de quem ficou amigo, e o cardeal Roberto Bellarmino, que havia sido o inquisidor de Giordano Bruno, mas que reconheceu as suas descobertas.
Mas, também,
Conforme vimos na aula As Contribuições de Galileu e Newton - Parte 1, segundo Reis, Guerra e Braga (2006), o conhecimento de desenho, especialmente do chiaroscuro, que Galileu adquiriu em Florença, lhe possibilitou compreender a aparência da Lua melhor do que seu antecessor Thomas Harriot, que também fez observações da Lua com uma luneta, no ano de 1609.
Segundo esses autores, a geometrização da projeção das sombras pode lhe ter permitido perceber as irregularidades da superfície lunar, permitindo-lhe, até mesmo, determinar a altura das montanhas lunares, novamente valendo-se da perspectiva.
Com isso, "a Lua representada por Galileu deixou de ser a imagem da perfeição – associada, no imaginário cristão, à Imaculada Conceição – e passou a ser mais um corpo celeste com características comuns, tal como a Terra. (REIS; GUERRA; BRAGA, 2006)
Em 1612, Galileu escreveu seu Discorso al serenissimo Don Cosimo Il Gran Duca di Toscana intorno alle cose, che stanno in su l'acqua, che in quella si muovono (Discurso sobre as coisas que estão sobre a água, ou que nela se movem). Nele menciona as manchas solares que observara e corretamente interpretara como matéria do próprio Sol, enquanto observadores anteriores, desde o astrônomo chinês Gan De, em 364 a.C., interpretavam como trânsitos do planeta Mercúrio. A variação das manchas, demonstrou a rotação do Sol,

No entanto, como vimos na aula Racionalismo e Empirismo - Parte 1, Galileu teve de enfrentar a Escolástica.

Na pintura acima, está representada claramente a postura do escolástico Cesare Cremonini que simplesmente se recusou a olhar pelo telescópio, alegando que nos livros de Aristóteles não havia qualquer menção a manchas solares e que, portanto, essas manchas não existiam!
Conforme dissemos na aula Racionalismo e Empirismo - Parte 1, Galileu se colocava como empirista.
Galileu rejeitou o Aristotelismo vigente. Nesse sentido, evita o 'porquê' do movimento, investigado desde Aristóteles, e concentra-se no 'como' (lei).
Antes, considerava-se Neoarquimediano, isto é, tal como Arquimedes, tinha uma visão física matemática, mais prática e menos filosófica.
"Após ter rejeitado a física de Aristóteles, após ter tentado, sem sucesso, construir ele mesmo uma física do senso comum, é uma física arquimediana o que Galileu vai doravante tentar fundar." (KOYRÉ, 1992, p. 98-99)
Tinha influência Neoplatônica, concebendo formas ideais para as coisas. Percebeu que, para estudar a queda dos corpos, teria que abstrair quaisquer interferências, tendo que trabalhar com objetos ideais (KOYRÉ, 1992, p. 96-98):
Quando Galileu “estuda o movimento no vazio, etc., ele coloca-se imediata e conscientemente fora da realidade. Um plano absolutamente liso, uma esfera absolutamente esférica, ambos absolutamente duros: são coisas que não se encontram na realidade física. Não são conceitos que se tirem da experiência.” (KOYRÉ, 1992, p. 98)
inaugurando, assim, conforme vimos na aula Realidade e Ciência - Parte 3, a distinção entre
No entanto, sabemos bem que
“são os seus conceitos 'fictícios' que nos permitem compreender e explicar a natureza, fazer-lhe perguntas, interpretar as suas respostas. (KOYRÉ, 1992, p. 98)
Porém, tal como dissemos, dissemos na aula Racionalismo e Empirismo - Parte 1, por falta de recursos tecnológicos para sua realização, várias experiências mencionadas por Galileu foram apenas experiências mentais (KOYRÉ, 1992). Por exemplo, a famosa experiência da Torre de Pisa não aconteceu (CROMBIE, 1957, p. 298).
Não dispondo de cronômetros de precisão, mas apenas rudimentares relógios d'água, Galileu tentou inicialmente usar seu pulso para marcar o tempo. Sem sucesso, concebeu o plano inclinado abaixo, que reduz a velocidade de queda do corpo. Depois, lembrando-se dos conhecimentos musicais que adquiriu com seu pai, que era alaudista, teve a idéia de utilizar a sensibilidade do ouvido humano aos batimentos no dispositivo com campainhas abaixo (DRAKE, 1975).

O corpo em queda pela canaleta fazia soar as campainhas à medida que passava por elas e estas podiam ser deslocadas ao longo do plano, alterando o intervalo de tempo entre seus toques. Ajustando cuidadosamente, conseguiu posicioná-las de forma que os intervalos fossem idênticos, quando observou que as distâncias entre elas cresciam de forma quadrática, o que deu base à sua Lei da Queda dos Corpos. (ver (CRAWFORD, 1996))
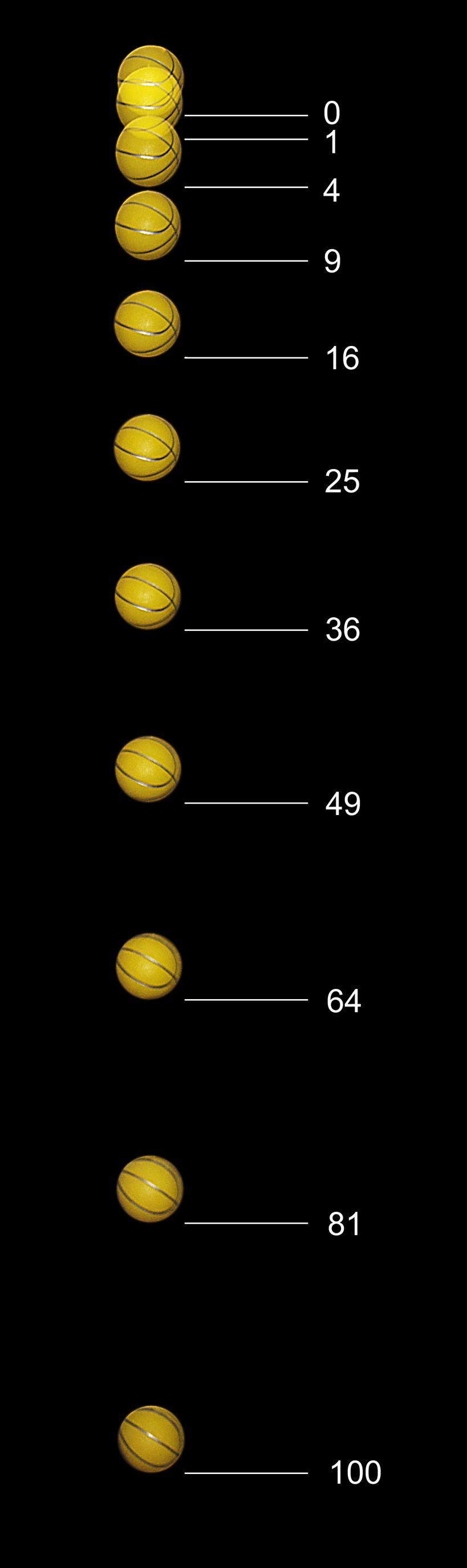
Na foto abaixo, um objeto em queda livre é fotografado com luz estroboscópica a intervalos de 1/20 de segundo e verifica-se que, de fato, as distâncias percorridas são proporcionais aos quadrados dos intervalos de tempo.
Com isso, Galileu geometrizou (matematizou) a Ciência, abandonando as discussões qualitativas, filosóficas.
No entanto, o Merton College (hoje pertencente à Universidade de Oxford) que incluía pensadores como Oresme e Ockham, só concebia 'variações' qualitativas, correspondentes a proporções geométricas (GRANT, 2002). Para eles, o conceito galileano de velocidade era inaceitável porque era um quociente de grandezas ontologicamente distintas: 'espaço' e 'tempo':
Reduzindo cada vez mais a inclinação do plano, Galileu chegou ao movimento em um plano horizontal. Ele observou que, nessas condições, o corpo nem se aproxima nem se afasta do chão, seu lugar natural, isto é, não realiza nem um movimento forçado nem um movimento natural, mas um terceiro tipo de movimento, não previsto por Aristóteles (DRAKE, 1964)!
Mais do que isso, observa que, nessas condições, o corpo tanto pode mover-se como não, indiferentemente. Galileu denominou esse movimento de movimento indiferente. Observou, também, que, em princípio, esse movimento poderia se estender infinitamente, desde que não se afastasse nem se aproximasse da Terra, antecipando, assim a idéia de inércia de Newton.
Desta forma, Galileu introduziu várias mudanças
Embora a Igreja aceitasse o Heliocentrismo como um modelo matemático, não o aceitava como realidade.
Galileu não tinha evidências para demonstrar a realidade do Heliocentrismo, o que não o impediu de escrever o Dialogo sopra i due massimi sistemi del mondo (Diálogo sobre os dois principais sistemas do mundo), considerada sua obra máxima, em que três personagens discutem sobre Mecânica:

No entanto, a disputa é desigual e Galileu usa de vários subterfúgios para vencer a discussão.
O mais grave, porém, é que intrigantes, incluindo o próprio cardeal Bellarmino, convenceram o Papa Urbano VIII de que o personagem simplório fora inspirado nele próprio. Ofendido, o papa, até então seu amigo e defensor, afastou-se e convocou a Inquisição para julgá-lo.

Doente, cansado e sem apoio, Galileu se vê obrigado a abjurar de suas idéias 'heréticas' e consegue a comutação da pena de prisão a confinamento domiciliar, embora seu Dialogo tendo sido incluído no o Index Librorum Prohibitorum, o Índice dos Livros Proibidos da Igreja Católica, bem como tendo sido proibida qualquer reedição dos seus livros. Diz a lenda que, à saída do tribunal, após sua condenação, disse a frase célebre "Eppur si muove!", ou seja, "apesar [de eu ter abjurado], ela se move", enfatizando que a verdade científica é empírica e não está sujeita à autoridade de ninguém.
Em 1642, Galileu morreu em casa, quase cego e sofrendo de hérnia.
Ferdinando II, Grão-Duque da Toscânia, queria sepultá-lo na Basílica de Santa Croce, próximo aos túmulos de seus antepassados e construir um mausoléu de mármore em sua honra. No entanto, o papa não permitiu pois, afinal, Galileu tinha sido condenado pelo Santo Ofício. Em vez disso, ele foi sepultado numa pequena sala lateral da Basílica.

Somente em 1835 seus livros foram retirados do Index.
Em 1992, o Papa João Paulo II lamentou publicamente o caso Galileu e reconheceu o erro da Igreja em o ter condenado.
Em 2008, declarou-se um plano de erigir uma estátua de Galileu no interior do Vaticano para comemorar o 400º aniversário das primeiras observações astronómicas, mas, um mês depois, o plano foi cancelado.
"Nossa nova cultura deve seu desenvolvimento ao fato de Newton ter nascido no ano da morte de Galileu" (Whitehead)
Veja também estas páginas:
 vídeo
Galileu: Batalha pelo Céu
vídeo
Galileu: Batalha pelo Céu vídeo
Ginga (Galáxia)
vídeo
Ginga (Galáxia) vídeo
Bohemian Rhapsody, Queen
vídeo
Bohemian Rhapsody, QueenReferências
Veja aqui minha aula sobre As Contribuições de Galileu e Newton
Voltar a Biografias.
Voltar a História da Física.
Voltar a Física Mecânica.
Voltar ao começo desta página
Voltar à página principal de Física Interessante