Segundo Roque,
"O século XVII é visto como a 'alvorada da matemática moderna', título do capítulo que H. Eves dedica ao período em sua Introdução à história da matemática" (ROQUE, 2012, p. 278).
Como vimos na aula História da Epistemologia - Parte 1, porém, segundo Roque (2012),
"A partir do século XVI, a história foi escrita, muitas vezes, com o intuito de mostrar que os europeus são herdeiros de uma tradição já européia, desde a Antiguidade" (ROQUE, 2012, p. 20).
Ainda segundo Roque (2012),
"De acordo com as narrativas convencionais, a matematica europeia, considerada a matemática tout court, originou-se com os gregos entre as épocas de Tales e Euclides, foi preservada pelos árabes no início da Idade Média e depois levada de volta para seu lugar de origem [sic], a Europa, entre os séculos XIII e XV, quando chegou à Itália pelas mãos de fugitivos vindos de Constantinopla. [...] Ora, com base nas evidências, não é possível sequer estabelecer uma continuidade entre as matemáticas mesopotâmica e grega. [...] Isso indica que talvez não possamos falar de evolução de uma única matemática ao longo da história, mas da presença de diferentes práticas que podemos chamar de 'matemáticas' segundo critérios que também variam" (ROQUE, 2012, p. 20).
Roque relata também que o próprio Bartel Leendert van der Waerden, matemático e historiador da Matemática e da Física, em seu livro Science Awakening (Despertar da Ciência), de 1950 mas ainda uma referência,
"[...] depois de elogiar Newton, [...] resume quase 2 mil anos de história em uma única frase: 'Em suma, todos os desenvolvimentos que convergem no trabalho de Newton, os da matemática, da mecânica e da astronomia, começam na Grécia'" (ROQUE, 2012, p. 24).
Como vimos na aula As Contribuições de Galileu e Newton, nas Universidades medievais, o ensino era baseado nas sete artes liberais e dividido em duas fases:
Segundo Roque (2012),
"A matemática era estudada para ajudar na compreensão das proposições aristotélicas sobre a lógica e a natureza; a aritmética consistia em regras de cálculo; a geometria era tirada de Euclides e de outras geometrias práticas; a música era influenciada por Boethius; e a astronomia seguia a tradição de Ptolomeu e das traduções dos trabalhos árabes" (ROQUE, 2012, p. 280).
De tal estudo, resultaria uma das três principais formações oferecidas: Medicina, Direito e Teologia, esta a soberana sobre todas as Ciências, como sugere a figura abaixo.
from
Grammar,
part of ‘Margarita Philosophica’ by Gregor Reisch
(1467?-
1525). First printed in 1503.Segundo Roque (2012),
"Na universidade, a matemática ainda era vista como parte da cultura antiga, a ser adimirada, mas não praticada" (ROQUE, 2012, p. 296).
Apesar disso, no século XVI, os artesãos e engenheiros interessaram-se pela matemática porque precisavam resolver problemas dinâmicos, levando-os a fazer pesquisas sobre balística, bombas de água e outros assuntos ligados à vida comum e, como diz Roque (2012),
"Comparado a Aristóteles, Arquimedes representava uma abordagem bem mais convincente para a compreensão desse tipo de problema" (ROQUE, 2012, p. 296).
Enxergava-se o renascimento da matemática como um renascimento da cultura antiga. Desde o século XIII eram traduzidos para o latim textos gregos, como os de Euclides, Arquimedes, Apolônio e Diofanto. No entanto, a Europa ocidental só começou a se apropriar dos trabalhos de Arquimedes no século XVI (ROQUE, 2012, p. 289-295).
Embora as interpretações anacrônicas de Neugebauer e de van der Waerden postulem que os babilônicos já possuíam rudimentos de Álgebra (ROQUE, 2012, p. 34),
"Pode-se dizer que a álgebra tem origem no estudo sistemático dos métodos para classificar e resolver equações, o que teve lugar com os trabalhos árabes iniciados por Al-Khwarizmi" (ROQUE, 2012, p. 248).
fonte:
al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wa-l-muqābala,
de Al-Khwarizmi, (830). Disponível em:
http://img.historiadigital.org/2010/01/Idade-Media-Algebra.jpg
Viète,
também conhecido como Franciscus
Vieta, seigneur de la
Bigotière, foi um matemático e advogado
francês.Como tantos outros de seu tempo, a despeito de todos os seus sucessos, a matemática era somente um passatempo para ele, cuja ocupação principal era ser um administrador público e advogado nas cortes de Carlos IX, Henrique III e Henrique IV.
Sua obra mais famosa é a In artem analyticem Isagoge (Introdução à arte analítica), de 1591, primeiro dos dez tratados incluídos na sua Opere restituæ Mathematicæ Analyseos, Seu, Algebrâ nouâ, (Obras de análise matemática restauradas, ou, Álgebra nova).
Embora a Álgebra já fosse utilizada pelos contemporâneos de Viète, "esse uso era fragmentado e não seguia um padrão unificado" (ROQUE, 2012, p. 298). "Como métodos algébricos não eram apresentados na forma axiomática-dedutiva dos Elementos de Euclides, [...] a questão da legitimidade desses procedimentos algébricos vinha à tona" (ROQUE, 2012, p. 299).
"[...] buscando usar a ferramenta analítica para resolver qualquer tipo de problema, Viète procurou fazer da álgebra uma ciência nos moldes gregos, apresentando-a de maneira axiomática" (ROQUE, 2012, p. 299).
"Viète não via a álgebra [...] como uma técnica concernindo números, mas como um cálculo simbólico concernindo grandezas abstratas. [...] Com esse propósito, introduziu letras para simbolizar grandezas indeterminadas, bem como grandezas desconhecidas" (BOS, apud ROQUE, 2012, p. 299).
Trinta e quatro anos após a morte de Vieta, o filósofo Descartes publicou um livro de Geometria que mudou a paisagem da álgebra, com base no trabalho de Vieta, aplicando-a a geometria. Acusado por Jean Baptiste Chauveau, explicou, em uma carta a Mersenne, que ele 'nunca teria lido essas obras'.
Em suas cartas a Mersenne, Descartes conscientemente minimizou a originalidade e profundidade do trabalho de seus predecessores, dizendo "Eu comecei onde Vieta parou".
Napier
foi um filósofo natural, astrólogo e
teólogo escocês.Napier é mais conhecido por ter criado os logaritmos neperianos, de base 1/e, também incorretamente chamados de logaritmos naturais, de base e, que se relacionam com aqueles por
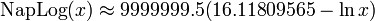
onde ln x é o logaritmo natural e NapLog(x) é o logaritmo neperiano.
Seu livro Mirifici Logarithmorum Canonis Descriptio, de 1614, continha não apenas uma explicação teórica dos logaritmos e tabelas de logaritmos, mas também, uma excelente discussão sobre trigonometria esférica. Esse trabalho propiciou avanços científicos na Astronomia, na Física e até na Astrologia. Tycho Brahe foi um dos seus primeiros utilizadores, como vimos na aula As Contribuições de Galileu e Newton. A contribuição dos logaritmos para a Revolução Científica foi importante pois simplificou os cálculos manuais, transformando multiplicações em somas, dispensando tabuadas.
Também ficou famoso por popularizar o ponto decimal e pelo dispositivo de cálculo que ficou conhecido como ossos de Napier
Consistiam
em um conjunto de bastões quadrangulares de
madeira, com
tabelas de multiplicação gravadas nas faces
laterais. Após a
justaposição dos bastões corretos, o
resultado da multiplicação se
fazia por uma simples leitura. Note-se, porém, que, embora
eles não
fossem baseados nos logaritmos, sua evolução
levou às réguas de cálculo
utilizadas por décadas até o aparecimento das
calculadoras eletrônicas.
Continue
conhecendo a Revolução na Matemática.Voltar à Parte Anterior
Voltar a Minhas Aulas.
Voltar ao começo desta página
Voltar à página principal de Física Interessante
