

Talvez você já tenha topado algum dia com um tesseract, o cubo em quatro dimensões, sem dar por isso. Não conseguimos ver em 4D mas, por um processo construtivo, conseguimos ter uma boa idéia dele.
Comecemos pelo ponto. Os matemáticos dizem que ele é um objeto de dimensão 0.
Se deslocarmos o ponto em uma dimensão, por exemplo, para a direita, obtemos um segmento de reta.

Deslocando esse segmento de reta em uma 2ª dimensão, perpendicular àquela, por exemplo, para cima, obtemos um quadrado.
Deslocando esse quadrado em uma 3ª dimensão, perpendicular àquelas, por exemplo, para trás, obtemos um cubo 'comum'. No entanto, na tela do seu computador ou numa folha de papel, não há como desenhar 'para trás' da folha de papel. Os artistas florentinos do quatrocento desenvolveram a técnica da perspectiva, segundo a qual a 3ª direção é desenhada inclinada, por exemplo, a um ângulo de 45º. Com isso, todas as faces quadradas, exceto a 'da frente' e a 'de trás' serão representadas 'deformadas' como paralelogramos.
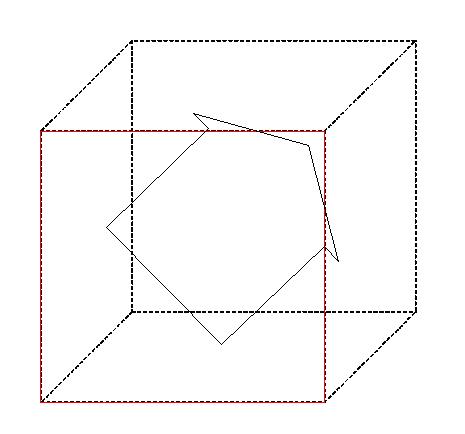
Finalmente, deslocando esse cubo em uma 4ª dimensão, perpendicular às anteriores, obtemos o cubo de 4 dimensões, isto é o tesseract. Como não sabemos representar essa 4ª dimensão, costuma-se representá-la 'para dentro' do cubo 'exterior'.
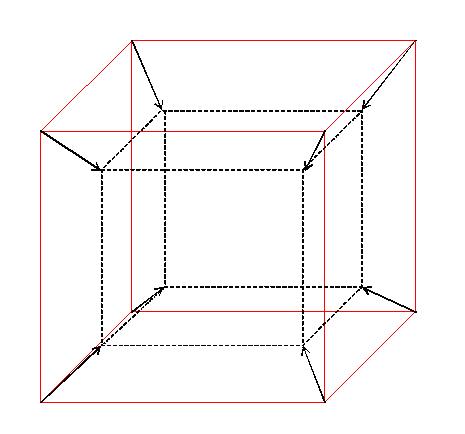
Como estará projetado num espaço de dimensão menor do que 4, todas as suas faces cúbicas, exceto a 'de fora' e a 'de dentro', serão vistas deformadas, como troncos de pirâmide.
Veja aqui o vídeo O Tesseract, em rotação. Imagine cubo de três dimensões, por exemplo um dado, em rotação: cada vez que uma face vem 'para a frente', ela deixa de estar deformada por efeito da perspectiva e aparece como um quadrado. Da mesma forma, neste vídeo, cada vez que uma face do tesseract vem 'para a frente', ela aparece como um cubo, o 'cubo de fora'.
Agora, uma analogia para entender melhor o tesseract.
Primeiro,
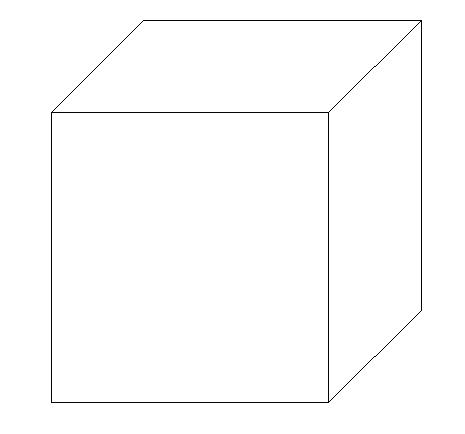
considere um cubo 'comum', em 3 dimensões.
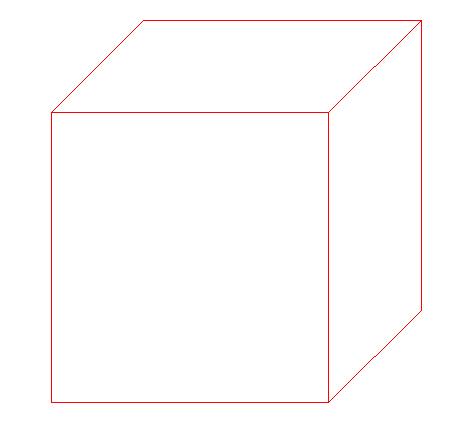
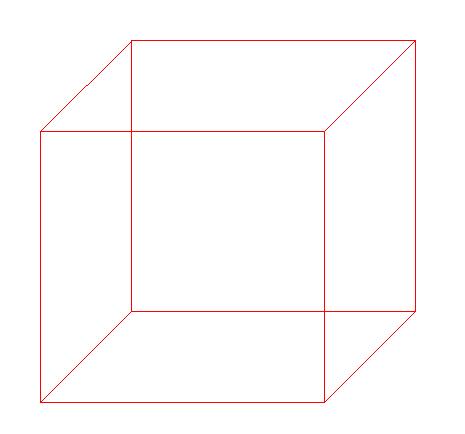
Um cubo tem 6 faces, sendo cada uma um quadrado. No entanto, devido a estar desenhado em uma superfície de 2 dimensões, todas as faces, exceto a 'da frente' e a 'de trás' aparecem deformadas, como paralelogramos.
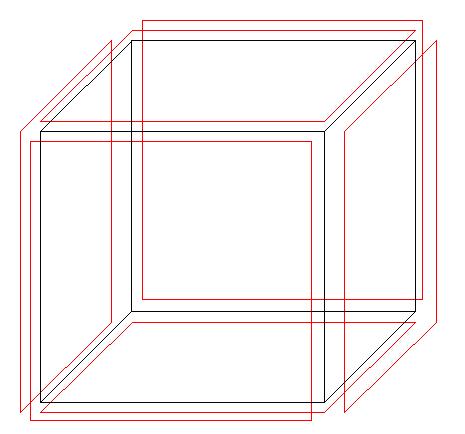
As faces adjacentes unem-se em 12 arestas, que são segmentos de reta.
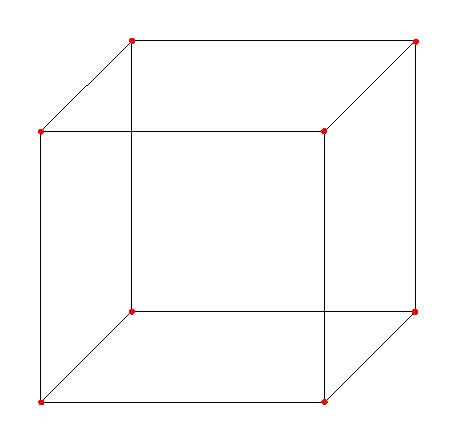
As arestas encontram-se, três a três, nos 8 vértices, que são pontos.
Os desenvolvimentos do cubo no plano e do tesseract no espaço de 3 dimensões são como nas figuras abaixo.
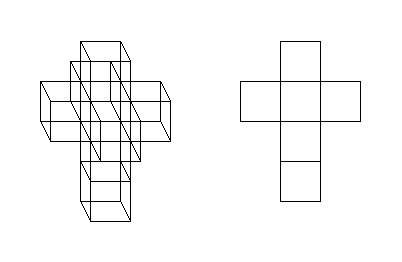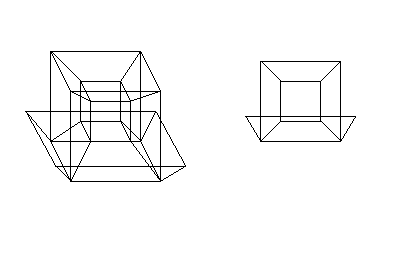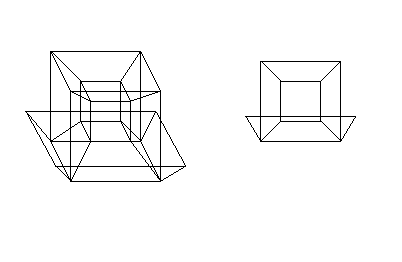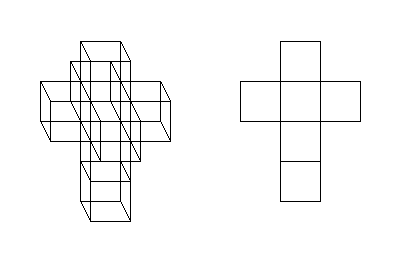
O cubo em 4 dimensões dimensão menor. E que a aresta, um segmento de reta, da mesma forma, pode ser pensada como um cubo em 1 dimensão, 2 dimensões menor, enquanto o vértice, um ponto, é um cubo em 0 dimensão, 3 dimensões menor.
Resumindo, o cubo de 3 dimensões terá
Analogamente, o cubo de 4 dimensões terá
Como estará projetado num espaço de dimensão menor do que 4, todas as suas faces, exceto as da frente e de trás, serão vistas deformadas. Como não conseguimos representar bem a 4ª dimensão, geralmente representamos o cubo que é a face da frente como por fora e o que é a face de trás como por dentro, como no desenho abaixo. Os cubos que são as outras faces aparecem deformados, como dito, como troncos de pirâmide.
O tesseract (desdobrado) apareceu, na arte, por exemplo, na obra ‘Corpus Hypercubus’ (1954) de Salvador Dali.

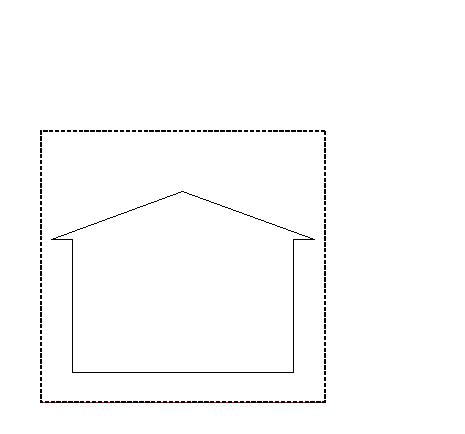
É, também, imprescindível mencionar o conto "E ele construiu uma casa torta" (1941) de Robert A. Heinlein, disponível na coletânea A Sonda do Tempo - As Ciências na Ficção Científica, de Arthur C. Clarke. Neste, um arquiteto constrói uma casa de oito cômodos com o formato da figura abaixo.

Mas um dia ocorre um terremoto e ... acontece o inesperado. Idéia que aparece no filme canadense de ficção científica Cube (Cubo) (1997) de Vicenzo Natali.

Finalmente, observe que, se o cubo não for transparente, e o olharmos bem de frente, só veremos a face da frente, como um quadrado.

Analogamente, se o tesseract não for transparente, e o olharmos bem 'de frente' com relação à 4ª dimensão, só veremos a face 'da frente', como um cubo 'comum'.
Conclusões:
Veja de novo o vídeo O Tesseract, em rotação.
Veja também esta página:
Veja aqui minha aula sobre A Crise da Física no inicio do século XX.
Voltar a Física Relatividade.
Voltar ao começo desta página
Voltar à página principal de Física Interessante